Delaunay triangulations of generalized Bolza surfaces
Résumé
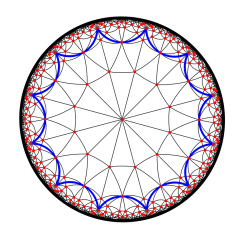
The Bolza surface can be seen as the quotient of the hyperbolic plane under the action of the group generated by the hyperbolic isometries identifying opposite edges of the regular octagon in the Poincaré disk that is centered at the origin. We consider generalized Bolza surfaces Mg, where the octagon is replaced by the regular 4g-gon, leading to a genus g surface. We propose an extension of Bowyer's algorithm to these surfaces. In particular, we compute the value of the systole of Mg; we also propose algorithms computing sets of points on Mg whose Delaunay triangulation is a simplicial complex.
Domaines
Géométrie algorithmique [cs.CG]
Fichier principal
 generalized_Bolza-hal.pdf (6.13 Mo)
Télécharger le fichier
generalized_Bolza-hal.pdf (6.13 Mo)
Télécharger le fichier
 genus3-2.png (200.24 Ko)
Télécharger le fichier
genus3-2.png (200.24 Ko)
Télécharger le fichier
| Origine | Fichiers produits par l'(les) auteur(s) |
|---|
| Format | Figure, Image |
|---|
